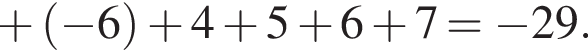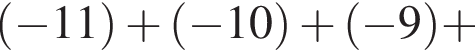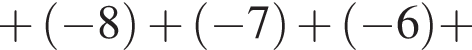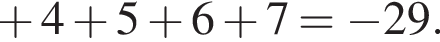1. Задание № 230 

Сложность: II
Классификатор алгебры: 4\.2\. Неравенства первой и второй степени относительно показательных функций
Показательные неравенства
i
Найдите наибольшее целое решение неравенства 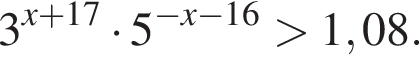
Решение. Решим неравенство:
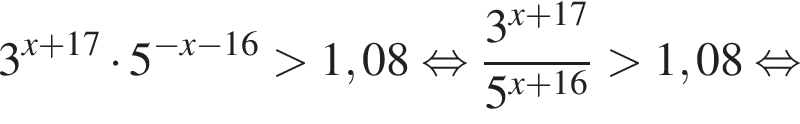
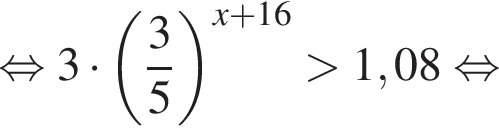
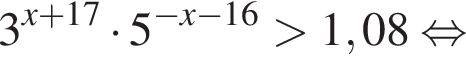
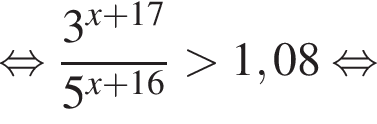
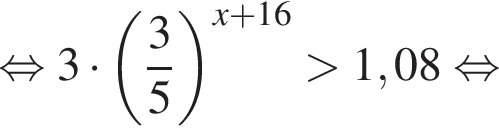
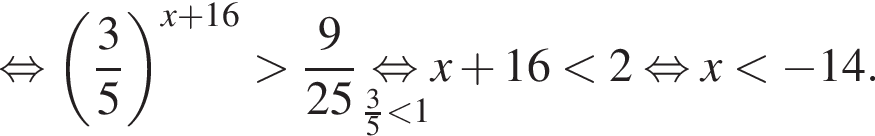
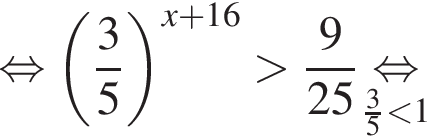
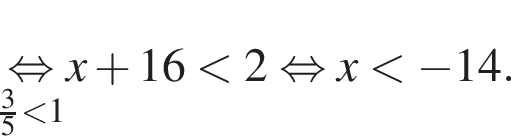
Таким образом, наибольшим целым решением неравенства является число −15.
Ответ: −15.
Ответ: -15
230
-15
Сложность: II
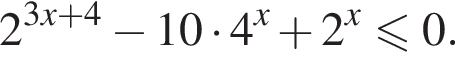
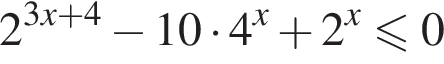
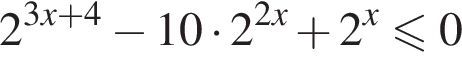
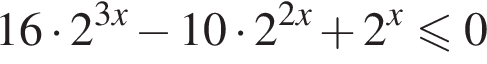
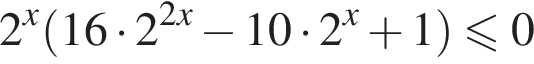
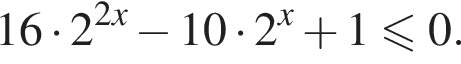
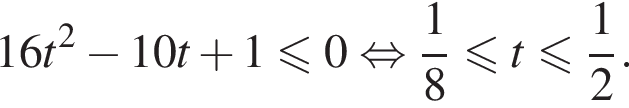
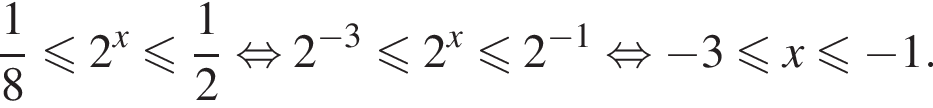
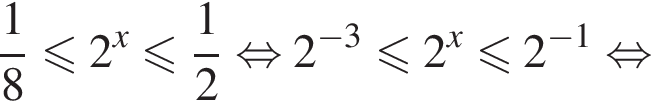

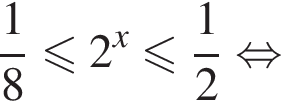
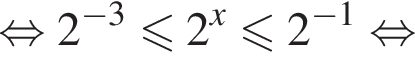
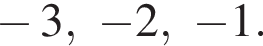 Их сумма равна −6.
Их сумма равна −6.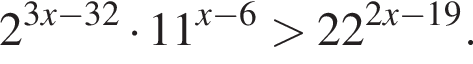
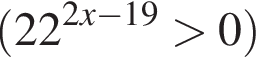 :
: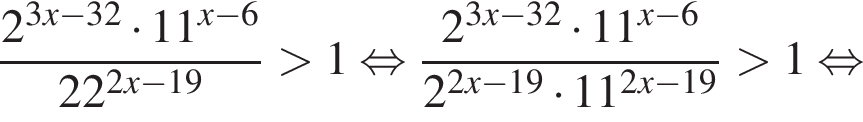
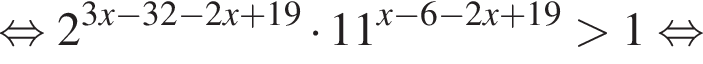
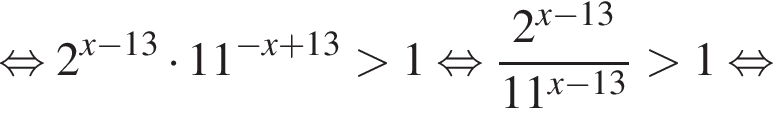
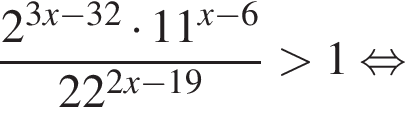
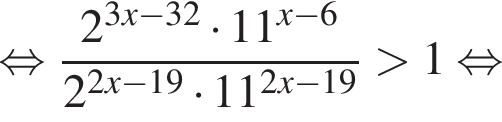
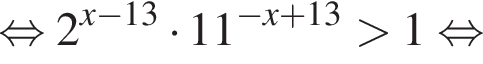
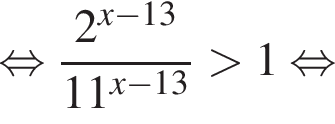
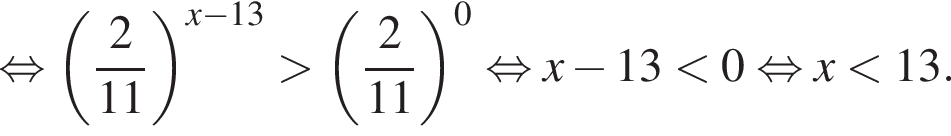
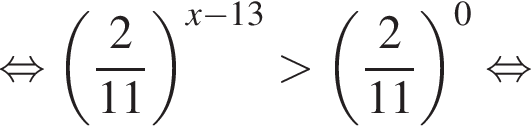
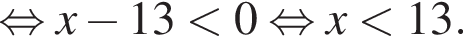
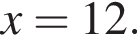
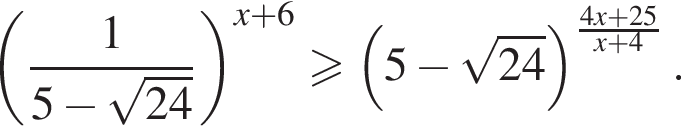 В ответе запишите сумму целых решений, принадлежащих промежутку [−20; −2].
В ответе запишите сумму целых решений, принадлежащих промежутку [−20; −2].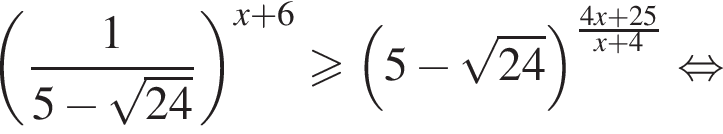
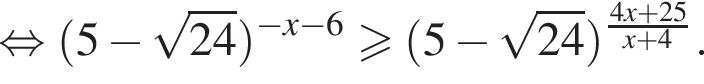
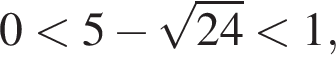 неравенство будет выполняться при
неравенство будет выполняться при 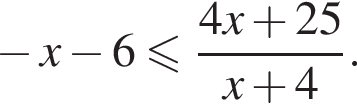 Имеем:
Имеем: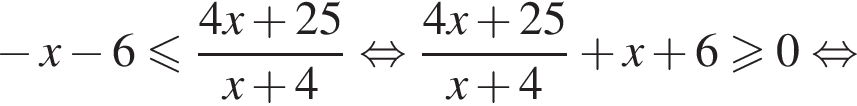
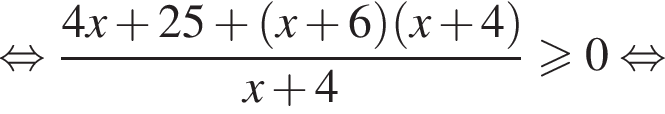
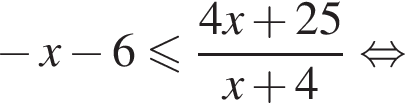
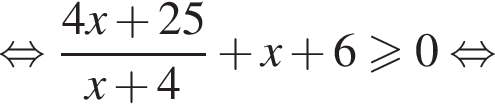
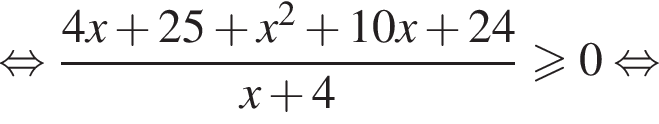
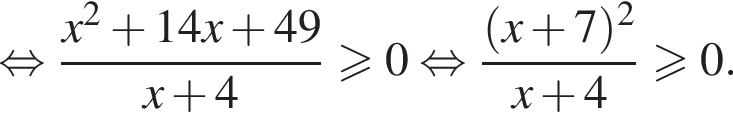
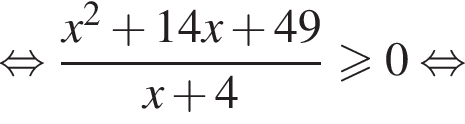
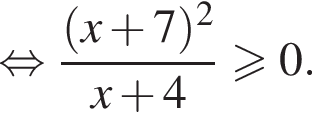
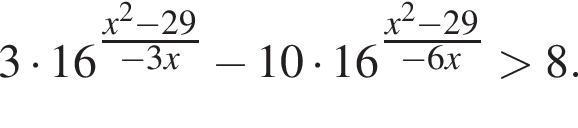
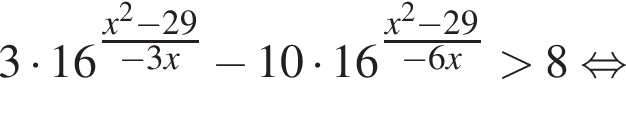
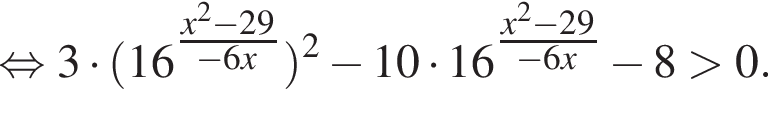
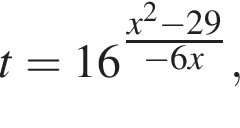 тогда имеем:
тогда имеем: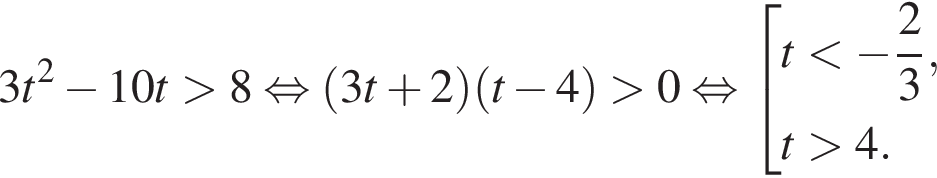
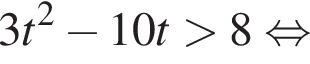
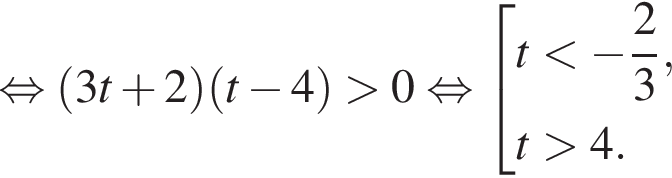
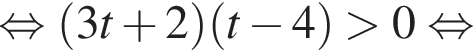
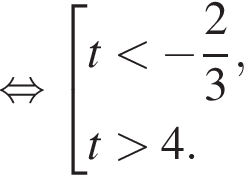
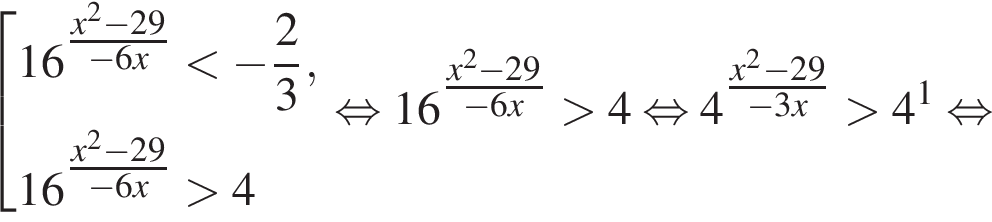
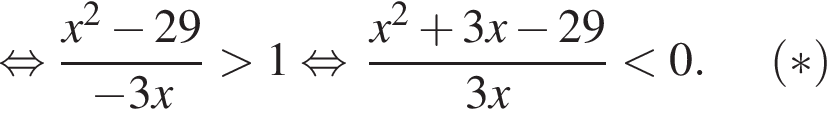
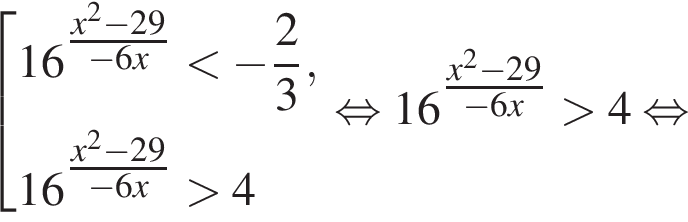
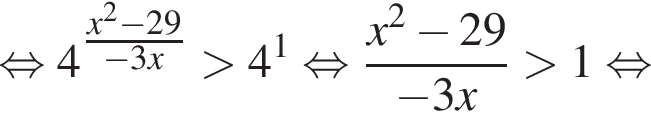
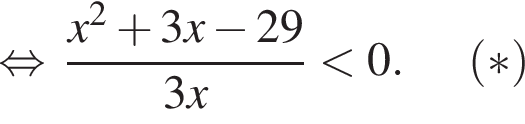
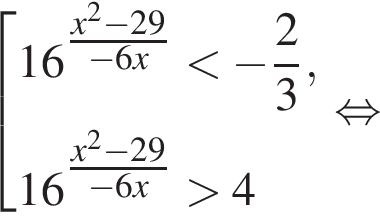
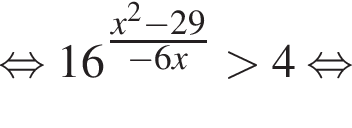
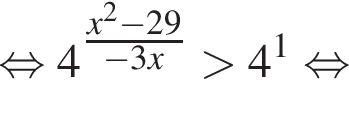
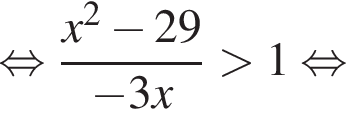
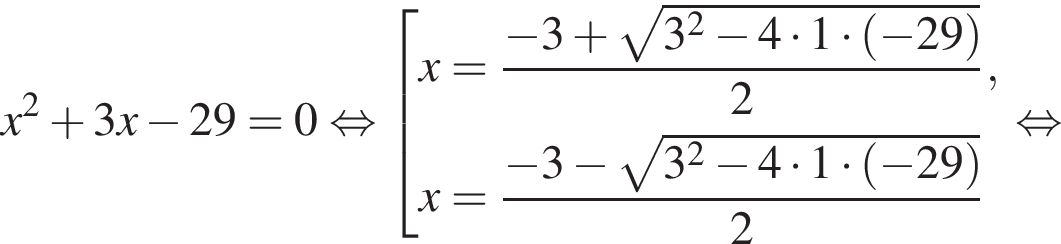
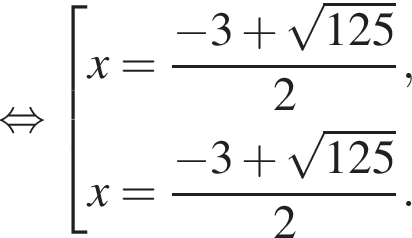
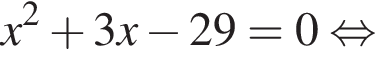
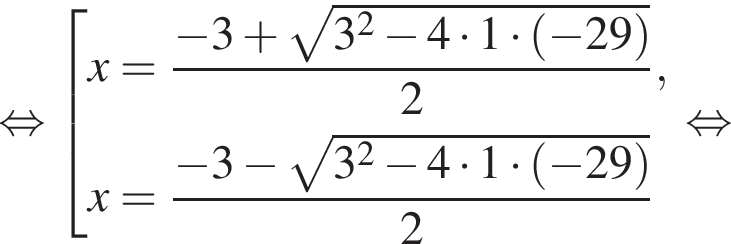
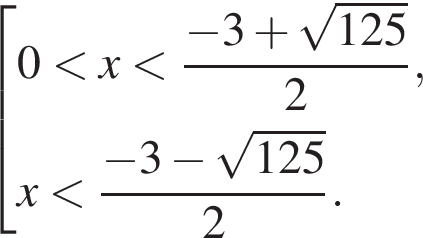
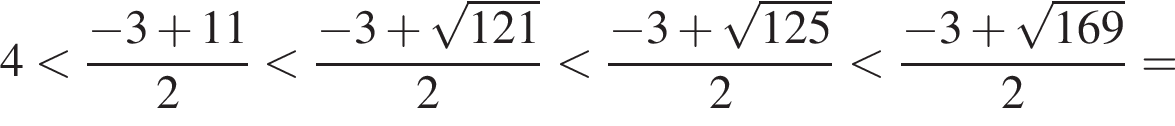
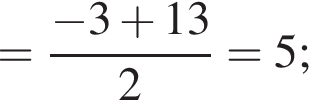
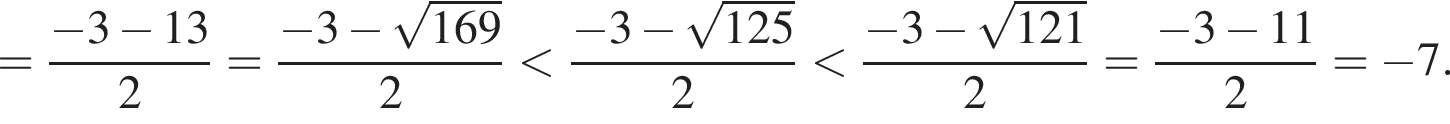

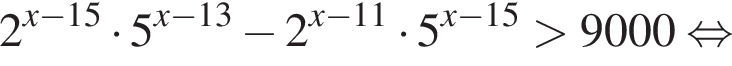
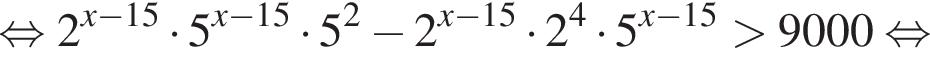

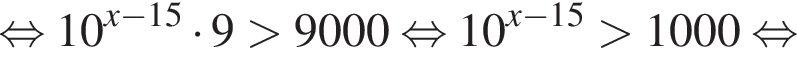
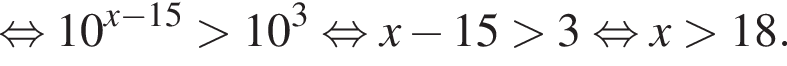
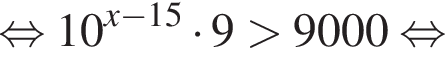

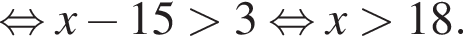
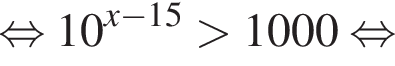
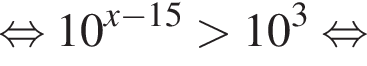
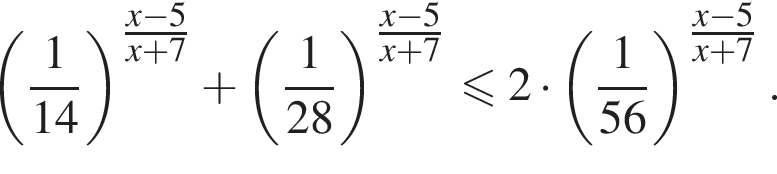
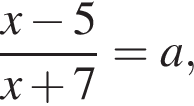 тогда
тогда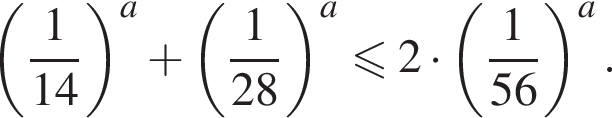
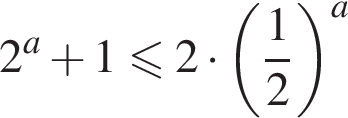
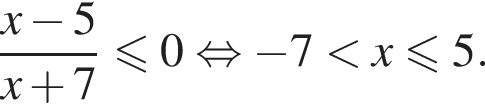
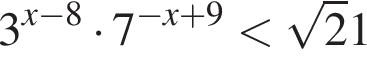 на промежутке (−16; 16).
на промежутке (−16; 16).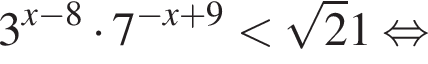
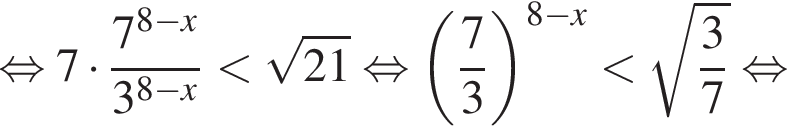
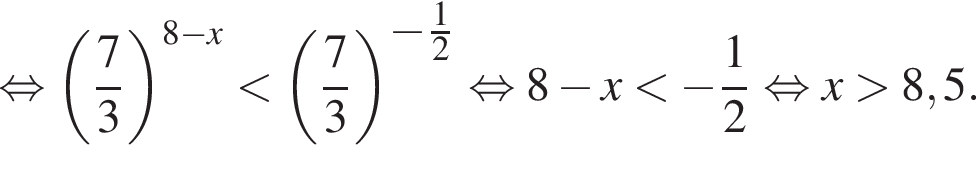
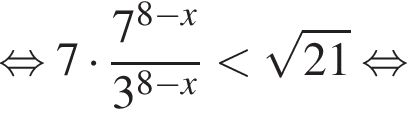
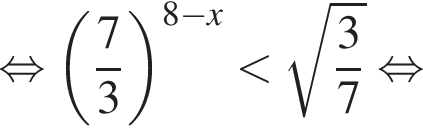
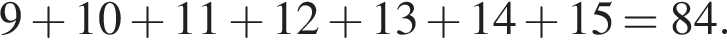
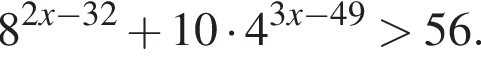
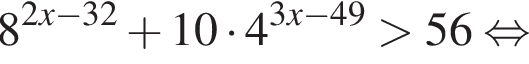
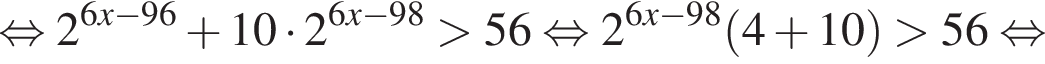
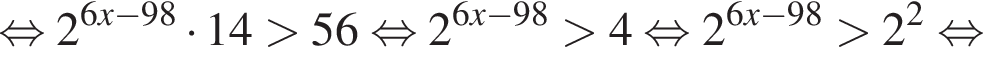
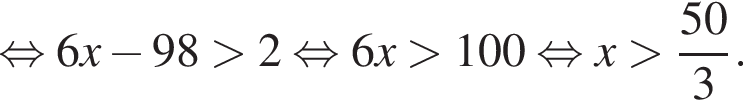
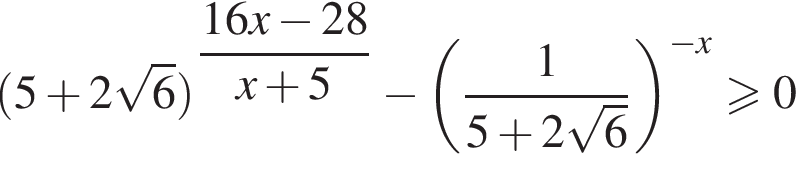
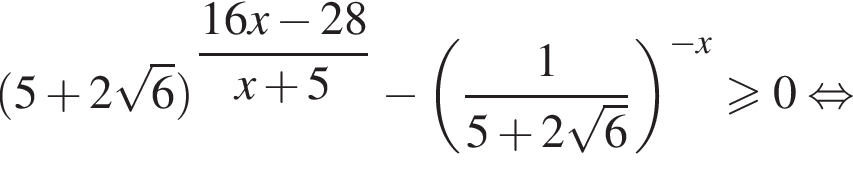
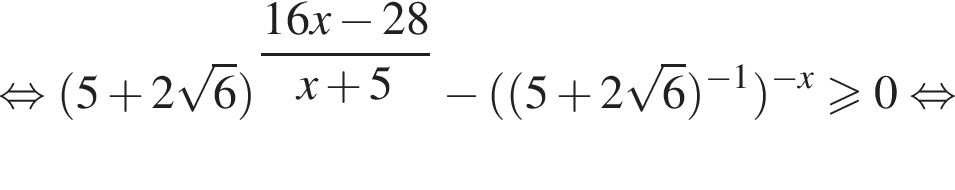
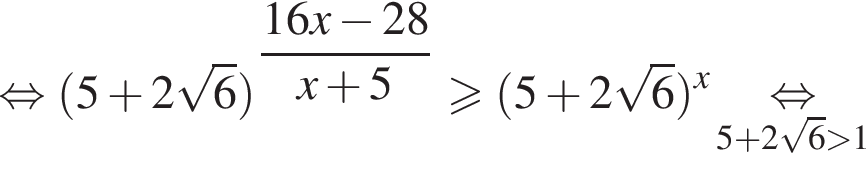
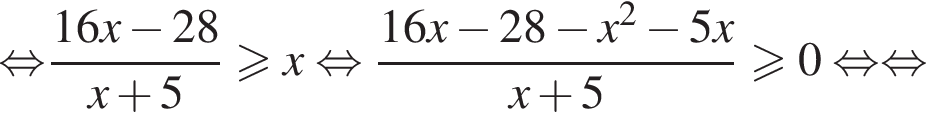
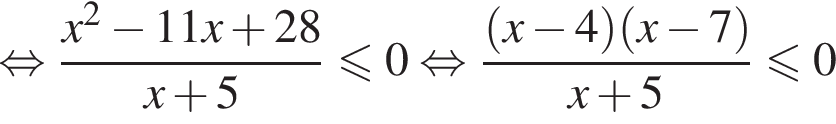
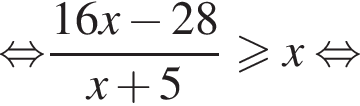
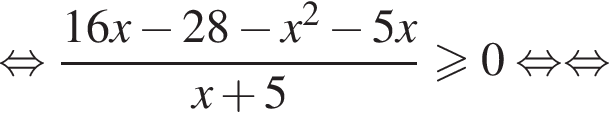
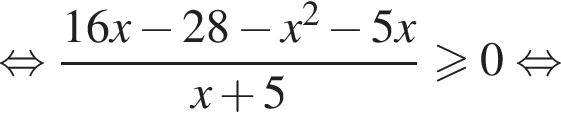
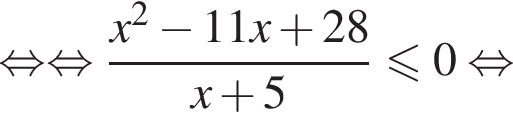
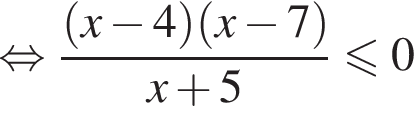
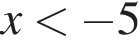 или
или 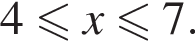 Найдем сумму целых решений неравенства, принадлежащих промежутку (–12; 12):
Найдем сумму целых решений неравенства, принадлежащих промежутку (–12; 12):